Các thủ tục thống kê dựa trên giả định về tính chuẩn trong dân số để thực hiện phân tích. Thông thường, các phương pháp kiểm định như t-test và F-test được coi là đáng tin cậy và không bị ảnh hưởng nghiêm trọng bởi sự khác biệt về tính chuẩn và tính đồng nhất của phương sai. Vì tính đáng tin cậy chung của các phương pháp này, nhiều nhà nghiên cứu không đề cập đến hình dạng phân phối trong bài báo của họ. Tuy nhiên, nhiều tác giả đã chỉ ra rằng việc chỉ báo cáo trung bình và độ lệch chuẩn của phân phối mà không đề cập đến độ lệch và độ nhọn có thể dẫn đến những suy luận thống kê sai lầm, đặc biệt khi kích thước mẫu nhỏ hoặc mức ý nghĩa thống kê rất nhỏ và dữ liệu bị sai lệch.

Việc kiểm tra các ngoại lệ và tính chuẩn là một bước quan trọng sơ bộ trong nhiều thủ tục thống kê suy luận. Một cách đơn giản để kiểm tra sự khác biệt so với mức tính chuẩn cơ bản trong dân số là vẽ biểu đồ phân phối của các điểm mẫu. Từ biểu đồ, ta có thể xác định các giá trị ngoại lệ và hình dạng chung của một phân phối, từ đó biết liệu nó có bị lệch hay không và có độ lệch dương hay âm.

Trong quá trình vẽ biểu đồ phân phối của các điểm mẫu, thường xuyên xác định các giá trị độ lệch và độ nhọn. Những giá trị này có thể được sử dụng để kiểm tra sự khác biệt đáng kể của phân phối so với mức chuẩn.

2. Nhận diện tính chính xác

Có nhiều phương pháp để đánh giá một phân bố tiêu chuẩn.

(1) Một cách đơn giản nhất để xem biểu đồ là sử dụng đường cong chuẩn, với hình dạng giống một chiếc chuông đối xứng. Tần số cao nhất nằm ở giữa và tần số giảm dần ở hai bên. Giá trị trung bình (mean) và trung vị (mediane) gần như bằng nhau và độ nghiêng (skewness) gần bằng không.

(2) Vẽ đồ thị chuẩn hóa xác suất (normal Q-Q plot). Biểu đồ này thể hiện mối quan hệ tuyến tính (đường thẳng) của phân phối chuẩn.

Khi kích thước mẫu lớn hơn 50, chúng ta sử dụng phép kiểm định Kolmogorov-Smirnov để kiểm tra phân phối chuẩn. Trong khi đó, khi kích thước mẫu nhỏ hơn 50, chúng ta sử dụng phép kiểm định Shapiro-Wilk. Một mẫu được coi là có phân phối chuẩn nếu mức ý nghĩa (p) lớn hơn 0.05.

(4) Mặc dù thử nghiệm Shapiro-Wilk và thử nghiệm Kolmogorov-Smirnov có thể được sử dụng để kiểm tra phân phối chuẩn với các mẫu nhỏ đến trung bình (nhỏ hơn 300), nhưng chúng không thể tin cậy cho các mẫu lớn. Thay vào đó, thử nghiệm độ lệch (skewness) và độ nhọn (kurtosis) có thể được sử dụng để xác định phân phối chuẩn cho các mẫu lớn. Nếu giá trị tuyệt đối của độ lệch nhỏ hơn 2 và giá trị tuyệt đối của độ nhọn (proper kurtosis) nhỏ hơn 7, thì dữ liệu có thể được cho là tuân theo phân phối chuẩn. Đáng chú ý là, thử nghiệm SPSS tính kurtosis dư thừa bằng cách trừ 3 từ giá trị độ nhọn (proper kurtosis).

3. Phân loại một phân phối chuẩn trong SPSS

Đo lường hiệu quả việc giảng dạy đạo đức kỹ thuật thông qua một khóa học tâm lý học cho sinh viên đại học kĩ thuật đã được thực hiện bằng cách kiểm tra điểm số (lần 1) và sau đó (lần 2) của 347 sinh viên. Chúng ta cần kiểm tra tính chuẩn của điểm lần 1 và điểm lần 2.

(1) Vẽ đồ thị đường cong tiêu chuẩn

Bước 1: Truy cập vào Phân tích > Thống kê mô tả > Tần số….

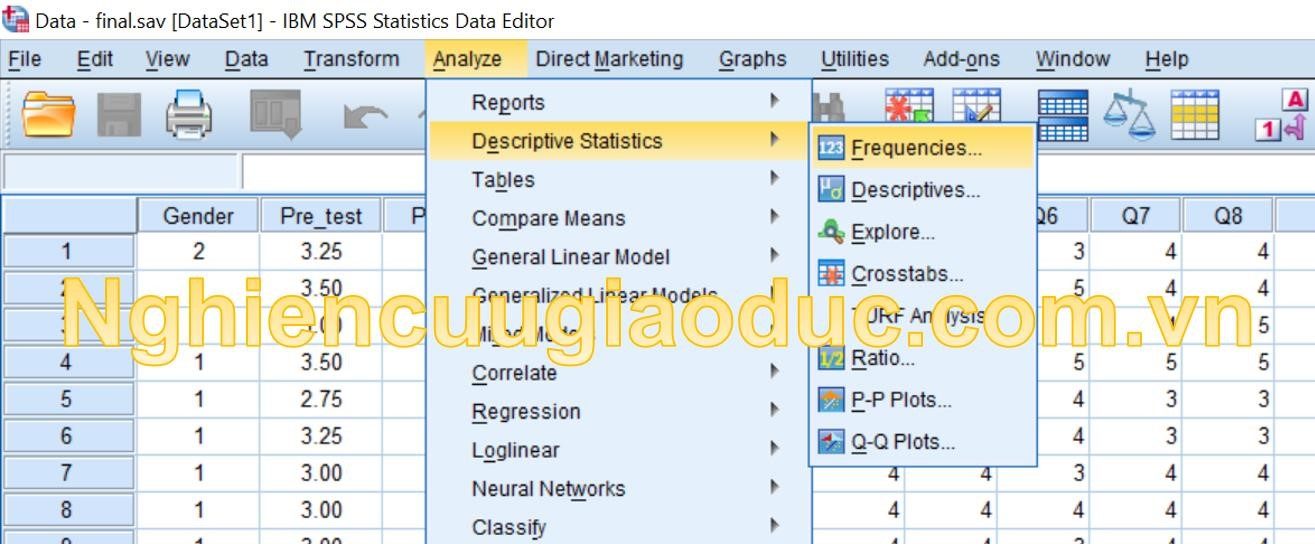
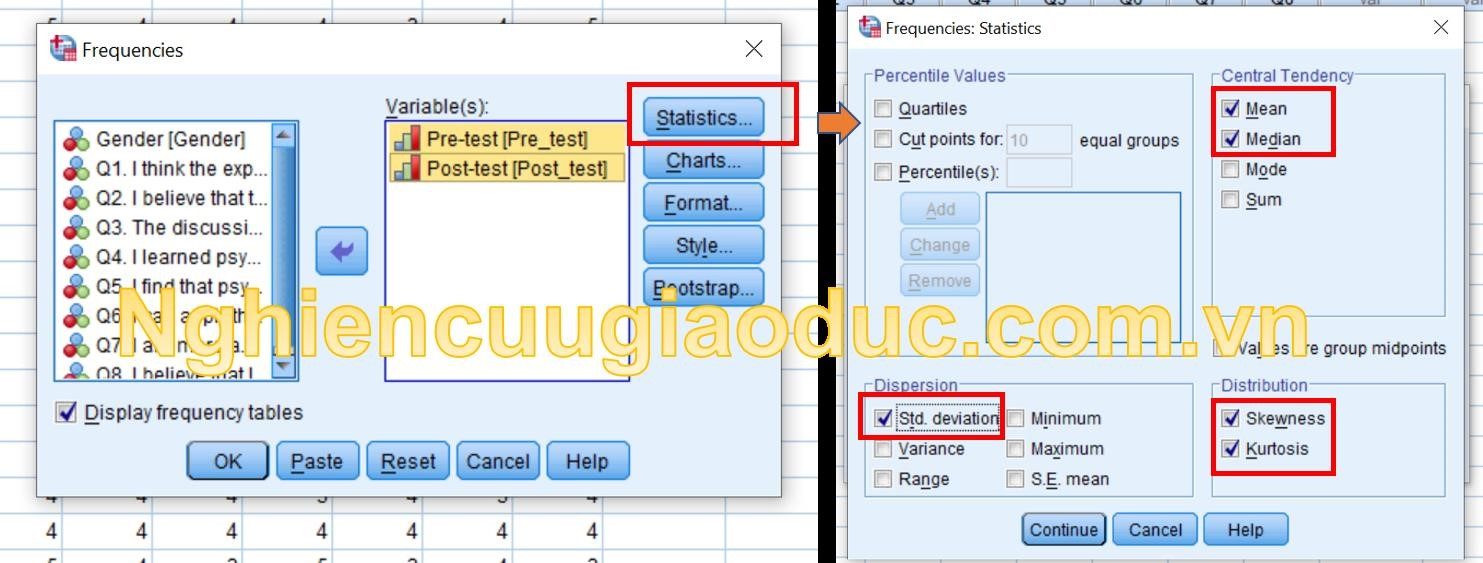
Bước 2: Trong hộp thoại Frequencies, di chuyển biến Pre-test và Post-test từ ô bên trái vào ô Variable(s). Bấm vào nút Statistics… Trên màn hình Statistics, đánh dấu vào 4 ô: Mean, Median, Std. Deviation, Skewness và kurtosis, và nhấp Continue.

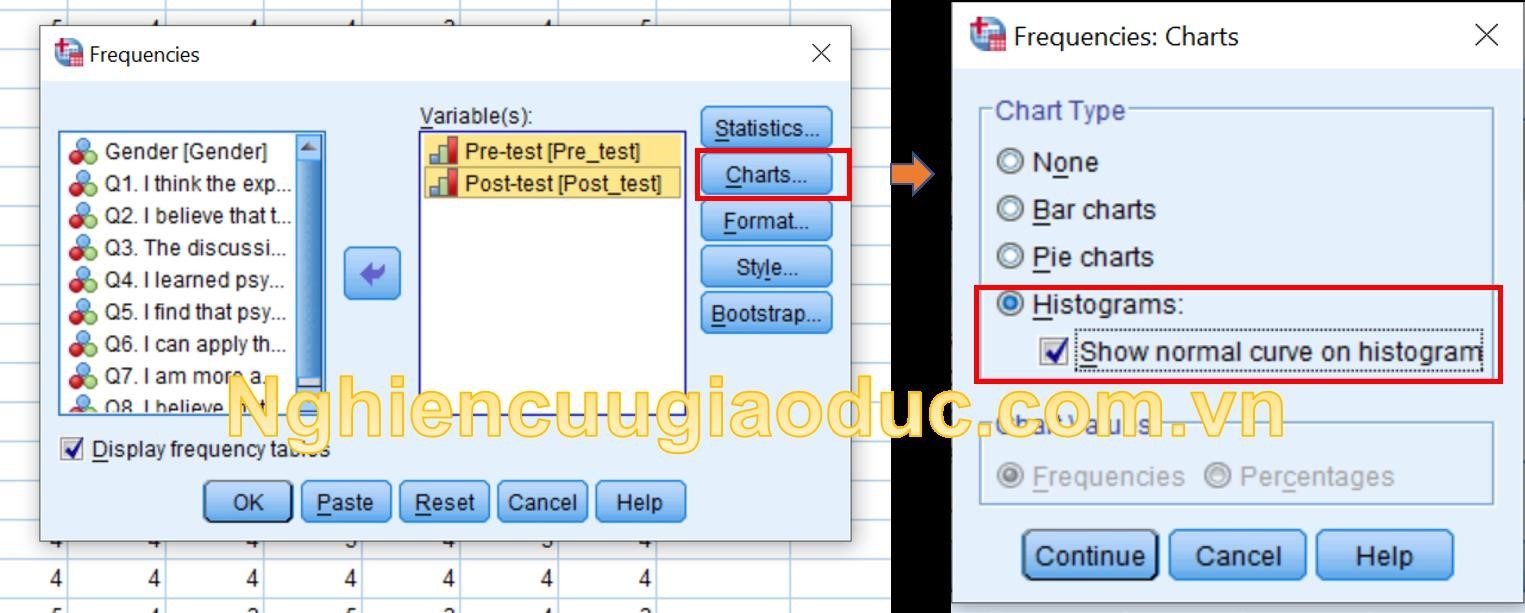
Tiến hành bước 3: Bấm vào nút Charts. Chọn ô tròn Histograms: và đánh dấu vào ô With Normal curve, sau đó nhấp Continue. Kết quả sau khi nhấn OK sẽ được hiển thị.

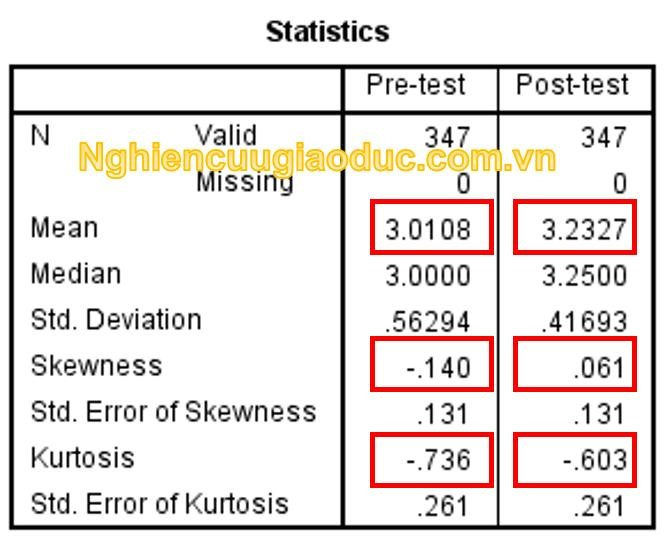
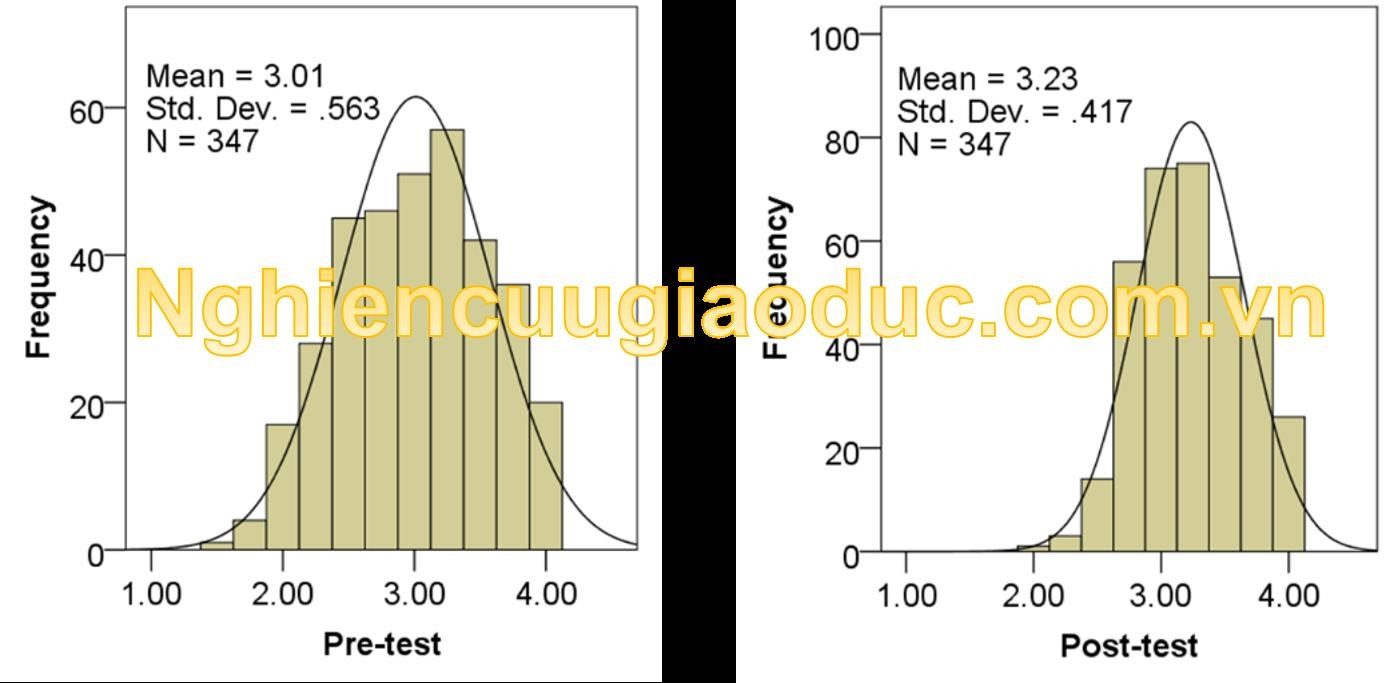
Trong Bảng Statistics, kết quả cho thấy điểm trung bình (mean) của lần 1 (Pre-test) là 3.01, trung vị (median) gần bằng nhau là 3.00. Vì vậy, có thể kết luận rằng đây là một phân phối chuẩn. Tương tự, điểm kiểm tra lần 2 cũng được cho là một phân phối chuẩn.

Dữ liệu thể hiện qua biểu đồ điểm số lần 1 và lần 2 có hình dạng giống hình chuông, và điểm số được phân bố đều ở cả hai phía của điểm trung bình. Điều này cho thấy khả năng của dữ liệu kiểm tra lần 1 và lần 2 tuân theo phân phối chuẩn.

(2) Vẽ đồ thị phân phối chuẩn và tiến hành kiểm định Kolmogorov-Smirnov/Shapiro-Wilk

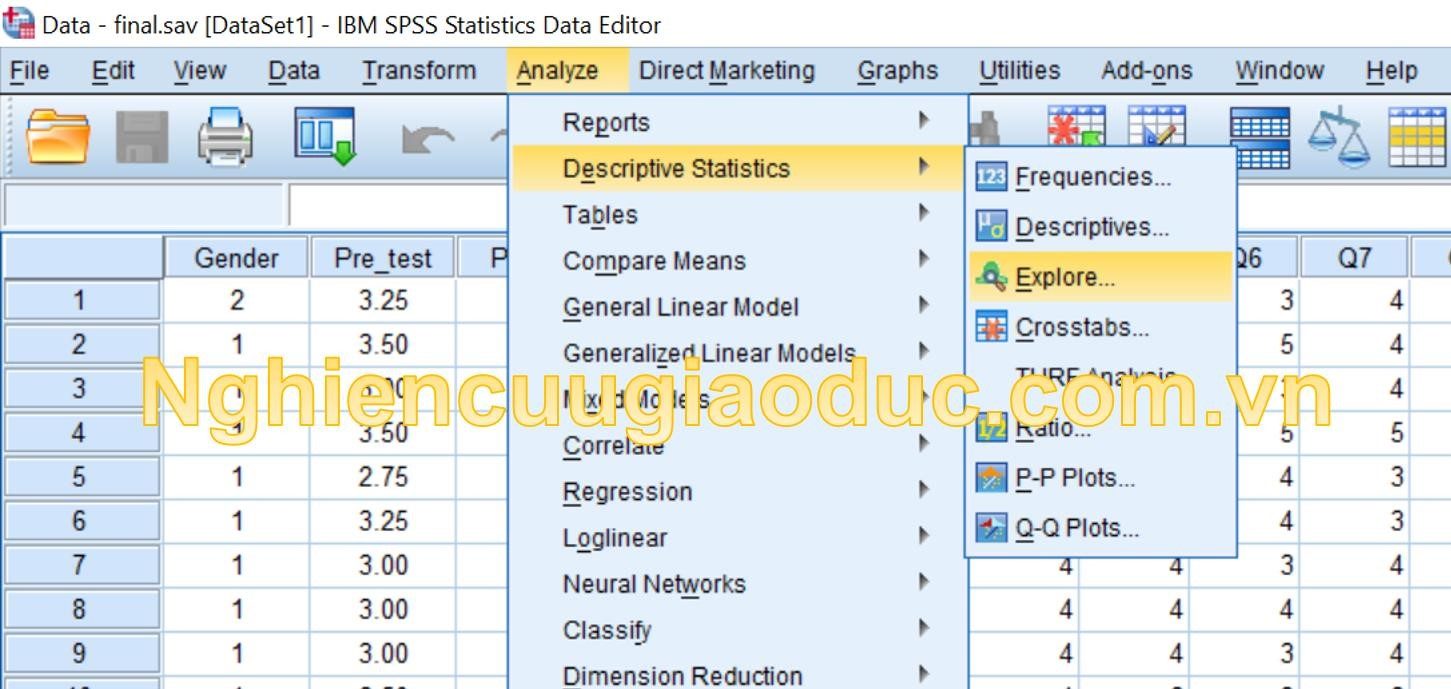
Bước 1: Để tạo biểu đồ phân phối chuẩn Q-Q (Normal QQ plot), chúng ta lựa chọn: Phân tích> Thống kê mô tả> Khám phá….

Bước 2: Khi hiển thị màn hình Khám phá, di chuyển Bài kiểm tra trước và Bài kiểm tra sau từ ô bên trái vào ô Danh sách phụ thuộc:.

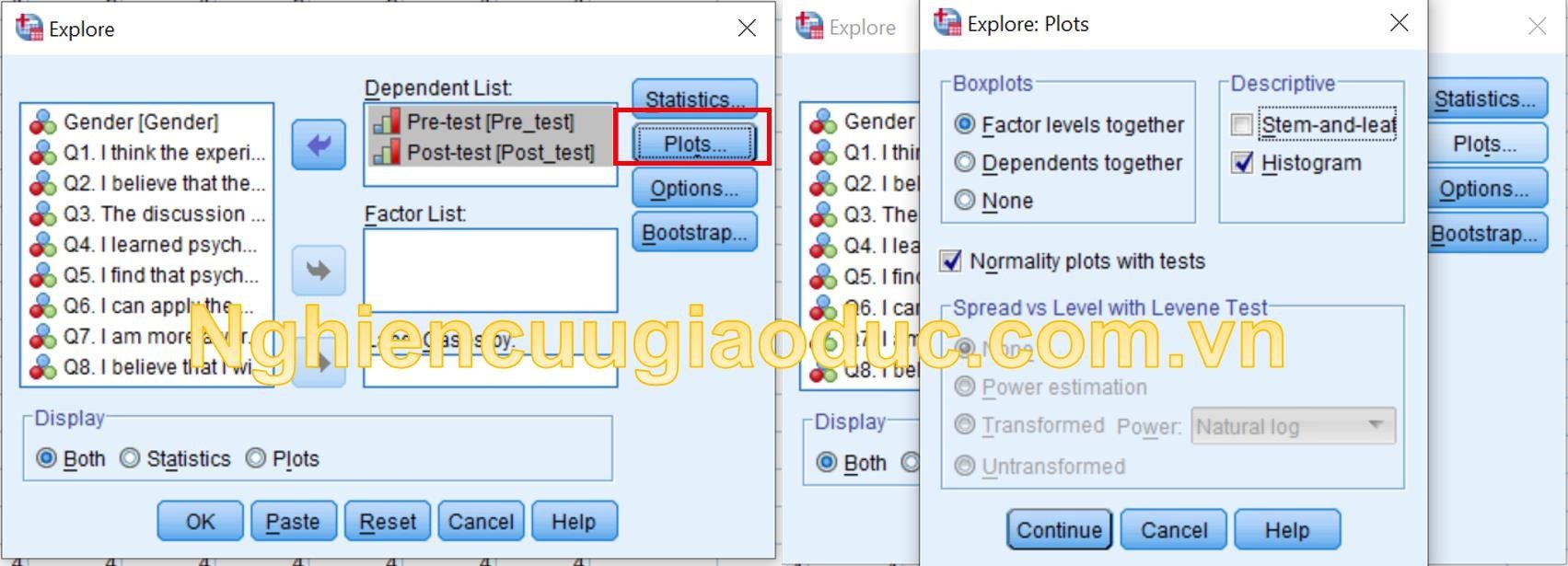
Tiếp theo, nhấp vào nút Plots trong bước thứ 3. Khi màn hình Explore: Plots hiện ra, hãy nhấp vào ô Histogram và ô Normality plots with tests. Sau đó, nhấp Continue và OK để xem kết quả hiển thị.

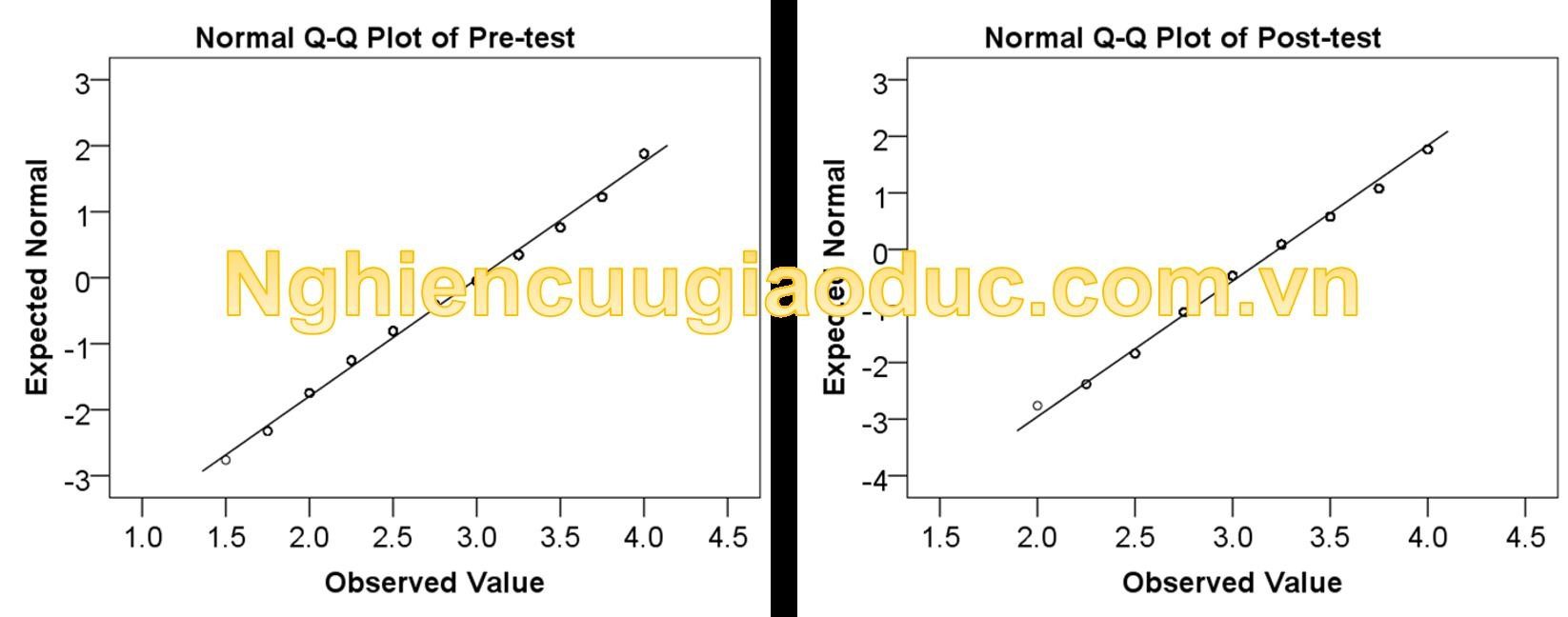
Xem biểu đồ Normal Q-Q Plot, các trị số quan sát và trị số mong đợi đều nằm gần trên đường thẳng.

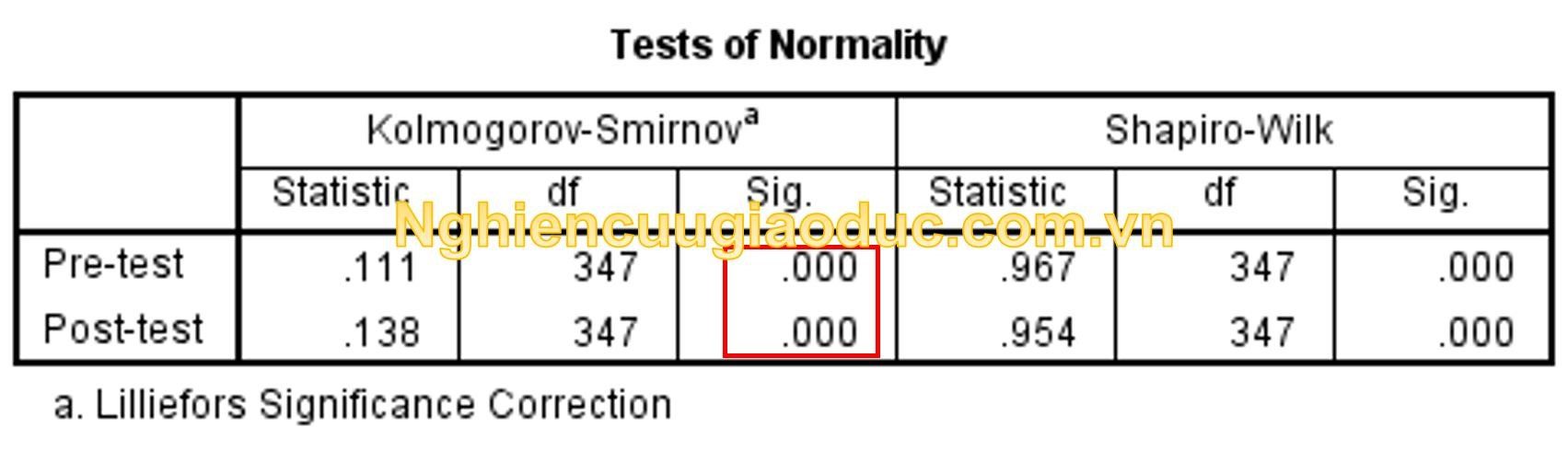
Do kích thước mẫu 345 lớn hơn 50, chúng ta sử dụng kết quả kiểm định Kolmogorov-Smirnov với Sig.= 0.00 như trong cả hai trường hợp. Điều này cho thấy phân phối không tuân theo chuẩn. Tuy nhiên, việc sử dụng thử nghiệm Shapiro-Wilk và thử nghiệm Kolmogorov-Smirnov để xác nhận phân phối chuẩn chỉ đáng tin cậy với các mẫu nhỏ đến trung bình, nhưng không đáng tin cậy với các mẫu lớn. Vì vậy, kết quả của thử nghiệm về độ lệch và độ nhọn có thể được sử dụng để xác định phân phối chuẩn cho các mẫu lớn.

Bảng Statistics cho thấy, nếu giá trị tuyệt đối của độ lệch (skewness) nhỏ hơn 2 và giá trị tuyệt đối của độ nhọn dư thừa (excess) nhỏ hơn 4, thì dữ liệu được cho là phân phối chuẩn.

Tóm lại, số liệu điểm kiểm tra lần 1 và lần 2 được phân phối theo định dạng chuẩn.